# Geo in GL part 1: Flattening Earth

It's my guilty pleasure to flatten the Earth. To put it on various planar surfaces: pages of paper, scrolls, billboards, screens. Many prominent people attempted that before me: Mercator and Cassini, just to name two.

Yes, I'm talking about maps and projections.

This is the first part of the story of how I used OpenGL shaders to project the Earth onto the flat computer screen. Here I introduce the reader to the basics of projections, write about the scope of my project, and then choose a projection that fits the scope.

**Warning**: if you believe the Earth is already flat, this blog post won't offer anything interesting for you. You might still be interested in the following parts in the series.

## What's the point?

I read someone online say shaders are bad for drawing maps: they aren't precise enough to distinguish distances a meter apart! Of course, I don't believe everything online, so I decided to check it myself, while refreshing my OpenGL knowledge, while playing with maps.

Which brings me to the next point.

## I like maps

While there are many representations of the real world, maps feel the most real. Some models turn the real into an unrecognizeable mess of abstract concepts. Maps are elegant, because they copy the real thing, just smaller. They aim to be recognizeable and familiar, so making them is always visually satisfying.

## Distortions

Maps are not perfect, though. They are not scale models, and they contain some abstract parts: a mountain represented on a map will be as flat as the paper or screen it's on. If it's marked, it will be either a drawing of a mountain, or a squiggle of height lines.

Most maps are also not globes. Our planet is round, and that means a flat map can't capture it accurately. Like a flattened orange peel, the map will get distorted: there will be tears or stretched places. The different ways to flatten the Earth to fit on a map are called *projections*.

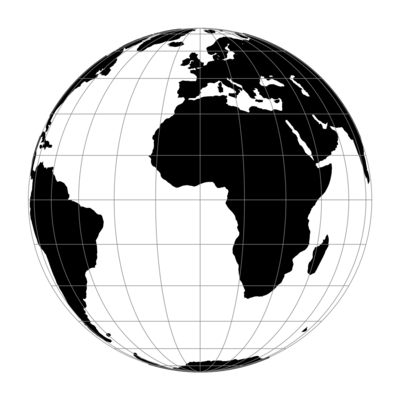This is also not a globe. It's just its picture! The picture is called *orthographic projection*.

## The scope

There are multitudes of projections available. To narrow it down, it helps to define what kind of maps are interesting in this project. With that in mind, the initial version of the program will

• display only small areas: not more than 100km in size. The smaller the area, the flatter the Earth surface, so distortions are smaller.
• Load a GPS track and display it as a squiggle. My GPS tracks are usually only a few hours long, and fit in the 100km size limit.
• Display nothing else. I don't want to get carried away and never prove what I set out to prove.

## Projection choices

The last big decision was to choose a projection.

### WGS84

Normally, we're used to seeing geographical coordinates of a point looking like: "*54,5°N 23,7°E*". This representation seems obvious. We live on a sphere, and so we use spherical coordinates. However, the prime meridian, and the precise measurement of the Earth axis, among oteher things, need to be standardized, so this representation is called WGS84. Since this is what GPS is using, it would be trivial to just plot the points from track on the screen as they are. However, the results would end up rather unappetizing:

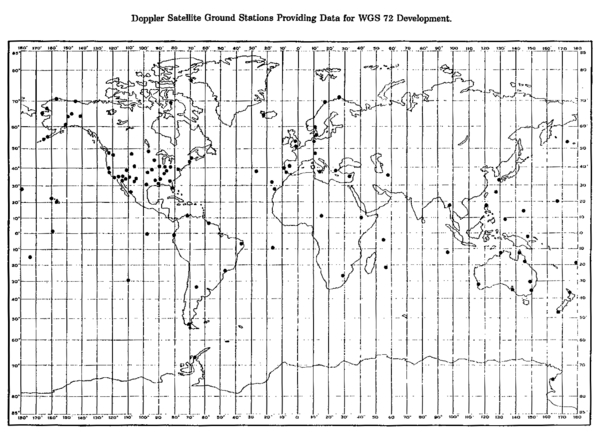
The distortions are huge! Can you see the grid sizes? Places at the equator are much smaller than at the poles, and the poles are extremely stretched sideways too – if you look at the globe, the grid is composed of wedges close to the poles. This would be a very unpleasant map to look at, even on our small scale.

### Mercator

The stretching is easily fixable by applying a varying stretching factor across the vertical position. This gives us the Mercator projection:

Image copyright Strebe, CC-BY-SA 3.0 Unported.

This projection is easy to calculate, and it covers most of the world, so it's very popular on the Internet. Most online maps use it, including OpenStreetMap's own osm.org. However, it's still rather bad: the stretching factor approaches infinity as we approach the poles, so the map doesn't have a top and bottom edge. Instead it's just cut off somewhere. The other problem is that the areas at the equator are still much smaller than near poles.

### Something different

It seems that both of those projections are quite bad at some places. But they are also both quite good at certain places: in this case, at the equator. So why don't we choose the best projection for our data?

That's what paper maps do. Unlike general purpose computer map viewers, paper maps are often limited to a small area on the Earth. They can focus on making this area undistorted, and they can ignore all the misshapen mess that's not printed on the paper. I deliberately chose to limit my program's area of interest to a 100km radius to take advantage of this.

For this, we need a projection that's not general like WGS84, or like the Mercator projection, but instead focussed on the area in question. To look at the North Pole in an undistorted way, we could choose the The North Pole Lambert Azimuthal Equal Area projection:

Here, I decided to increase my difficulty: I will not make an assumption about where on the Earth my GPS track is. It could be Europe, the Equator, or the Arctic. Instead, I will try to hit the bullseye and make sure that my projection favors the area I'm displaying, no matter what it is. For that, I need to find a family of projections that I can adjust.

Thankfully, people have come up with plenty of different ways of projecting:

Various projections: Alaska, Mollweide, Winkel I, van der Grinten (I), Gauss-Schreiber Transverse Mercator, Tobler-Mercator, International Map of the World Polyconic, Oblique Cylindrical Equal Area. (Images courtesy PROJ.)

Some of them are tweakable, to name a few: azimuthal equidistant, Cassini, gnomonic.

Most of them preserve shapes over small areas rather well, so the choice is not that important. Nevertheless, I'm not an expert, so it's possible that I'm underestimating distortions. To stay on the safe side, I choose the azimuthal equidistant, because it promises that distances from the central point can be measured with a ruler. I used it previously with an overlaid kilometer grid and it worked well.

Here's the projection in proj form, so you can apply it in QGIS. Don't forget to adjust `lat_0` and `lon_0` to your area of interest!

```
+proj=aeqd +lat_0=54 +lon_0=24 +x_0=0 +y_0=0 +a=6371000 +b=6371000 +units=m +no_defs
```

## Next steps

I have the projection, but I still don't know the math behind it, and don't have any code. Stay tuned for the next part!